** Progress in Earth and Planetary Science is the official journal of the Japan Geoscience Union, published in collaboration with its 51 society members.
** Progress in Earth and Planetary Science is partly financially supported by a Grant-in-Aid for Publication of Scientific Research Results to enhance dissemination of information of scientific research.
Gallery View of PEPS Articles
Research
Solid earth sciences
Session convener-recommended article JpGU Meeting 2015
201610201610
Reconstruction of a 2D seismic wavefield by seismic gradiometry
Maeda T, Nishida K, Takagi R, Obara K
seismic gradiometry, array signal processing, surface waves, scattering, numerical simulation
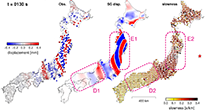
Wavefield and propagation direction analyzed by seismic gradiometry at elapsed times of t = 130 s. Each panel shows the observed vertical-component displacement amplitude (color scale) at stations in the 25–50 s period band (left), the continuous displacement wavefield reconstructed by seismic gradiometry (center), and propagation direction and its slowness estimated from the gradiometry parameters (right). The absolute value of slowness is shown by the color scale. Arrow length is proportional to the absolute value of the slowness. The star in the right panel shows the epicenter location.
You can also watch movies on the article page of SpringerOpen.
We reconstructed a 2D seismic wavefield and obtained its propagation properties by using the seismic gradiometry method together with dense observations of the Hi-net seismograph network in Japan. The seismic gradiometry method estimates the wave amplitude and its spatial derivative coefficients at any location from a discrete station record by using a Taylor series approximation. From the spatial derivatives in horizontal directions, the properties of a propagating wave packet, including the arrival direction, slowness, geometrical spreading, and radiation pattern can be obtained. In addition, by using spatial derivatives together with free-surface boundary conditions, the 2D vector elastic wavefield can be decomposed into divergence and rotation components. First, as a feasibility test, we performed an analysis with a synthetic seismogram dataset computed by a numerical simulation for a realistic 3D medium and the actual Hi-net station layout. We confirmed that the wave amplitude and its spatial derivatives were very well-reproduced for period bands longer than 25 s. Applications to a real large earthquake showed that the amplitude and phase of the wavefield were well reconstructed, along with slowness vector. The slowness of the reconstructed wavefield showed a clear contrast between body and surface waves and regional non-great-circle-path wave propagation, possibly owing to scattering. Slowness vectors together with divergence and rotation decomposition are expected to be useful for determining constituents of observed wavefields in inhomogeneous media.
