** Progress in Earth and Planetary Science is the official journal of the Japan Geoscience Union, published in collaboration with its 51 society members.
** Progress in Earth and Planetary Science is partly financially supported by a Grant-in-Aid for Publication of Scientific Research Results to enhance dissemination of information of scientific research.
Gallery View of PEPS Articles
Research
Solid earth sciences
201509201509
The competition between Lorentz and Coriolis forces in planetary dynamos
Soderlund K M, Sheyko A, King E M, Aurnou J M
Planetary dynamos, Core convection, Magnetic fields, Rotation, Magnetostrophic force balance
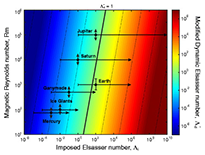
Lorentz to Coriolis force ratio predictions for planetary cores. Modified dynamic Elsasser number as a function of imposed Elsasser number and magnetic Reynolds number across a range of values that may be relevant to planets in our solar system as well as exoplanets. The approximate ranges of anticipated Λi and Rm values are given for planets with active dynamos. Barred line ends for Λi denote the observed magnetic field strength; arrowed line ends denote upper bounds. Barred line ends for Rm denote constrained bounds; arrowed line ends denote a larger range of uncertainties. Black circles denote the most probable Λi and Rm values.
Fluid motions within planetary cores generate magnetic fields through dynamo action. These core processes are driven by thermo-compositional convection subject to the competing influences of rotation, which tends to organize the flow into axial columns, and the Lorentz force, which tends to inhibit the relative movement of the magnetic field and the fluid. It is often argued that these forces are predominant and approximately equal in planetary cores; we test this hypothesis using a suite of numerical geodynamo models to calculate the Lorentz to Coriolis force ratio directly. Our results show that this ratio can be estimated by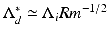 
(Λ i is the traditionally defined Elsasser number for imposed magnetic fields and Rm is the system-scale ratio of magnetic induction to magnetic diffusion). Best estimates of core flow speeds and magnetic field strengths predict the geodynamo to be in magnetostrophic balance where the Lorentz and Coriolis forces are comparable. The Lorentz force may also be significant, i.e., within an order of magnitude of the Coriolis force, in the Jovian interior. In contrast, the Lorentz force is likely to be relatively weak in the cores of Saturn, Uranus, Neptune, Ganymede, and Mercury.
