** Progress in Earth and Planetary Science is the official journal of the Japan Geoscience Union, published in collaboration with its 51 society members.
** Progress in Earth and Planetary Science is partly financially supported by a Grant-in-Aid for Publication of Scientific Research Results to enhance dissemination of information of scientific research.
Gallery View of PEPS Articles
Research
Human geosciences
201706201706
Eigenvector of gravity gradient tensor for estimating fault dips considering fault type
Kusumoto S
Fault dip, Gravity gradient tensor, Eigenvector, Normal fault, Reverse fault, Kurehayama fault
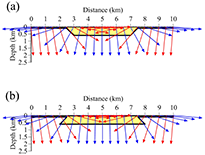
Eigenvectors of the gravity gradient tensor caused by the simplified sedimentary basin models. The maximum eigenvector and minimum eigenvector are indicated by red and blue, respectively. (a) Eigenvectors on the sedimentary basin formed by normal faults. The dip of the maximum eigenvector follows the dip of the normal fault. (b) Eigenvectors on the sedimentary basin are formed by reverse faults. The dip of the minimum eigenvector follows the dip of the reverse fault.
The dips of boundaries in faults and caldera walls play an important role in understanding their formation mechanisms. The fault dip is a particularly important parameter in numerical simulations for hazard map creation as the fault dip affects estimations of the area of disaster occurrence. In this study, I introduce a technique for estimating the fault dip using the eigenvector of the observed or calculated gravity gradient tensor on a profile and investigating its properties through numerical simulations. From numerical simulations, it was found that the maximum eigenvector of the tensor points to the high-density causative body, and the dip of the maximum eigenvector closely follows the dip of the normal fault. It was also found that the minimum eigenvector of the tensor points to the low-density causative body and that the dip of the minimum eigenvector closely follows the dip of the reverse fault. It was shown that the eigenvector of the gravity gradient tensor for estimating fault dips is determined by fault type. As an application of this technique, I estimated the dip of the Kurehayama Fault located in Toyama, Japan, and obtained a result that corresponded to conventional fault dip estimations by geology and geomorphology. Because the gravity gradient tensor is required for this analysis, I present a technique that estimates the gravity gradient tensor from the gravity anomaly on a profile.